基尔霍夫矩阵是用来求解生成树计数、求(权值)和相关题目的利器。
0. 求完全图的生成树数量(Prufer序列)
要说基尔霍夫矩阵,就要从一道题目说起:
给你 $n$,问 $n$ 个节点组成的无向无根树有多少种。
这道题可以用Prufer序列去做。
这里简单说一下Prufer序列的求法:
对于一张无向无根树,重复执行以下操作直到只剩 $2$ 个或更少的点,最后得到的那个序列 $a$ 就是这棵树的Prufer序列:
- 我们找到此时度为 $1$ 的节点,若有多个,找编号最小的,设找到的节点编号为 $x$。
- 在 $a$ 的末尾添加:与 $x$ 有连边的那个唯一节点。
- 删除 $x$。
Prufer序列别看求法非常简单,也没啥容易发现的性质,其实用处很大。
Prufer序列满足一个性质,就是,所有无向无根树,都可以唯一地对应一个Prufer序列;所有Prufer序列都可以唯一地对应一棵树。
所以,这道题就有解了,答案其实就是长为 $n-2$ 的Prufer序列有多少种。
由于Prufer序列的每个元素的值都是从 $1$ 到 $n$ 的,所以答案就是 $n^{n-2}$,显然。
1.1. 求任意无向图的生成树数量(基尔霍夫矩阵)
但如果把题目变化一下,就不能用Prufer序列去求了:
给你一张 $n$ 个节点 $m$ 条边的无向图,问这张图的生成树有多少个。
这题要用基尔霍夫矩阵。
具体地,我们定义 $D$ 矩阵,求法:
$ D_{i,j}= \begin{cases} 0 & i \not= j \ \text{deg}(i) & i=j \end{cases} $
其中,$\text{deg}(i)$ 代表这张图上 $i$ 的度是多少。
我们再定义 $A$ 矩阵,求法:
$ A_{i,j}= \begin{cases} \text{ecnt}(i,j) & i \not= j \ 0 & i=j \end{cases} $
其中,$\text{ecnt}(i,j)$ 代表这张图上点 $i$ 和点 $j$ 之间的边数。
然后,我们再定义基尔霍夫矩阵 $K=D-A$,即:
$ K_{i,j}= \begin{cases} -\text{ecnt}(i,j) & i \not= j \ \text{deg}(i) & i=j \end{cases} $
最后,我们同时删掉 $K$ 中的一行和一列(一般是删掉最后一行和最后一列,但删掉哪一行、哪一列答案都不变),此时 $K$ 的行列式即为本题答案。
(以下所有 $D$、$A$、$K$ 的求法都是一样的,答案求法也是一样的,所以只说 $\text{deg}$ 函数和 $\text{ecnt}$ 函数的求法)
*注:
如果是有向图生成树相关题目,且题目指定了根,那么删除的那一行和那一列的编号,必须是根节点的编号。
如,题目要求 $1$ 节点为根,那么删除的必须要是第一行和第一列,否则会WA。
此外,以下所有题里,在求 $\text{deg}$ 函数和 $\text{ecnt}$ 函数时,都要忽略自环。
并且,如果说下面构造的方阵没有行列式,那么就说明没有生成树,要输出 $0$。
1.2. 求任意无向带权图的生成树权值之和(基尔霍夫矩阵)
这题还有变种:
给你一张 $n$ 个节点 $m$ 条边的无向带权图,问这张图所有生成树的权值之和。
一棵生成树的权值定义为这棵生成树内所有边权之和。
$\text{deg}(i)$ 代表这张图上 $i$ 的所有出边的边权之和,$\text{ecnt}(i,j)$ 代表这张图上点 $i$ 和点 $j$ 之间所有边的边权和。
2.1.1. 求任意有向图的生成外向树数量(基尔霍夫矩阵)
但还没完,还有题目:
给你一张 $n$ 个节点 $m$ 条边的有向图,问这张图的生成树有多少个。
此处,生成树要求是外向树。
所谓外向树,就是一棵有向树,满足每条边都是从父亲指向儿子的。
$\text{deg}(i)$ 代表这张图上 $i$ 的入度,$\text{ecnt}(i,j)$ 代表这张图上从点 $i$ 连向点 $j$ 的边的数量。
2.1.2. 求任意有向带权图的生成外向树权值之和(基尔霍夫矩阵)
但还没完,还有题目:
给你一张 $n$ 个节点 $m$ 条边的有向带权图,问这张图的生成树的权值之和。
此处,生成树要求是外向树。
$\text{deg}(i)$ 代表这张图内连向 $i$ 的边权之和,$\text{ecnt}(i,j)$ 代表这张图上从点 $i$ 连向点 $j$ 的边权之和。
2.2.1. 求任意有向图的生成内向树数量(基尔霍夫矩阵)
但还没完,还有题目:
给你一张 $n$ 个节点 $m$ 条边的有向图,问这张图的生成树有多少个。
此处,生成树要求是内向树。
所谓内向树,就是一棵有向树,满足每条边都是从儿子指向父亲的。
$\text{deg}(i)$ 代表这张图上 $i$ 的出度,$\text{ecnt}(i,j)$ 代表这张图上从点 $i$ 连向点 $j$ 的边的数量。
2.2.2. 求任意有向带权图的生成内向树权值之和(基尔霍夫矩阵)
但还没完,还有题目:
给你一张 $n$ 个节点 $m$ 条边的有向带权图,问这张图的生成树的权值之和。
此处,生成树要求是内向树。
$\text{deg}(i)$ 代表这张图内 $i$ 的出边边权之和,$\text{ecnt}(i,j)$ 代表这张图上从点 $i$ 连向点 $j$ 的边权之和。
3. 求完全二分图的生成树个数(基尔霍夫矩阵拓展)
但还没完,还有题目:
给你两个数 $n$、$m$,问左边 $n$ 个点,右边 $m$ 个点的完全二分图的生成树个数。
这个问题可以被转化为问题1.1,所以我们就可以得到基尔霍夫矩阵:
$ \begin{bmatrix} m & 0 & \cdots & 0 & -1 & -1 & \cdots & -1 \ 0 & m & \cdots & 0 & -1 & -1 & \cdots & -1 \ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & m & -1 & -1 & \cdots & -1 \ -1 & -1 & \cdots & -1 & n & 0 & \cdots & 0 \ -1 & -1 & \cdots & -1 & 0 & n & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \ -1 & -1 & \cdots & -1 & 0 & 0 & \cdots & n \ \end{bmatrix} $
标一些参数:
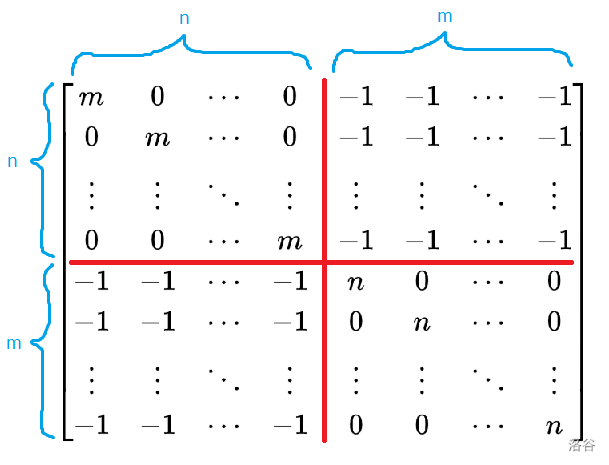
(图1)
然后,可以发现,在上面的划分方案中,左上部分和右下部分其实都是方阵,所以我们只要让左下部分全部变为 $0$ 就可以用行列式性质转化问题了。
进而,既然求这个矩阵的行列式,我们就先把最后一行和最后一列去掉,即把图1的参数内的两个 $m$ 改成 $m-1$。
我们既然要把左下部分变成 $0$,我们就要变化矩阵。
我们首先把矩阵前 $n$ 行全部除以 $m$,得到:
$ \large \begin{bmatrix} 1 & 0 & \cdots & 0 & \frac{-1}{m} & \frac{-1}{m} & \cdots & \frac{-1}{m} \ 0 & 1 & \cdots & 0 & \frac{-1}{m} & \frac{-1}{m} & \cdots & \frac{-1}{m} \ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & 1 & \frac{-1}{m} & \frac{-1}{m} & \cdots & \frac{-1}{m} \ -1 & -1 & \cdots & -1 & n & 0 & \cdots & 0 \ -1 & -1 & \cdots & -1 & 0 & n & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \ -1 & -1 & \cdots & -1 & 0 & 0 & \cdots & n \ \end{bmatrix} $
其次,算出前 $n$ 行矩阵之和:
$ \large \begin{bmatrix} 1 & 1 & \cdots & 1 & \frac{-n}{m} & \frac{-n}{m} & \cdots & \frac{-n}{m} \end{bmatrix} $
然后,对于后 $m-1$ 行,每一行都加上前 $n$ 行之和:
$ \large \begin{bmatrix} 1 & 0 & \cdots & 0 & \frac{-1}{m} & \frac{-1}{m} & \cdots & \frac{-1}{m} \ 0 & 1 & \cdots & 0 & \frac{-1}{m} & \frac{-1}{m} & \cdots & \frac{-1}{m} \ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & 1 & \frac{-1}{m} & \frac{-1}{m} & \cdots & \frac{-1}{m} \ 0 & 0 & \cdots & 0 & n-\frac{n}{m} & -\frac{n}{m} & \cdots & -\frac{n}{m} \ 0 & 0 & \cdots & 0 & -\frac{n}{m} & n-\frac{n}{m} & \cdots & -\frac{n}{m} \ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & 0 & -\frac{n}{m} & -\frac{n}{m} & \cdots & n-\frac{n}{m} \ \end{bmatrix} $
最后,把前 $n$ 行重新都乘上 $m$:
$ \large \begin{bmatrix} m & 0 & \cdots & 0 & -1 & -1 & \cdots & -1 \ 0 & m & \cdots & 0 & -1 & -1 & \cdots & -1 \ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & m & -1 & -1 & \cdots & -1 \ 0 & 0 & \cdots & 0 & n-\frac{n}{m} & -\frac{n}{m} & \cdots & -\frac{n}{m} \ 0 & 0 & \cdots & 0 & -\frac{n}{m} & n-\frac{n}{m} & \cdots & -\frac{n}{m} \ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & 0 & -\frac{n}{m} & -\frac{n}{m} & \cdots & n-\frac{n}{m} \ \end{bmatrix} $
此时左下角都是 $0$ 了。
于是乎,问题就转化为了以下两个矩阵的行列式之积:
$ D_1= \large \begin{bmatrix} m & 0 & \cdots & 0 \ 0 & m & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & m \end{bmatrix} $
$ D_2= \large \begin{bmatrix} n-\frac{n}{m} & -\frac{n}{m} & \cdots & -\frac{n}{m} \\ -\frac{n}{m} & n-\frac{n}{m} & \cdots & -\frac{n}{m} \\ \vdots & \vdots & \ddots & \vdots \\ -\frac{n}{m} & -\frac{n}{m} & \cdots & n-\frac{n}{m} \end{bmatrix} $
(注意,$D_2$ 是个 $(m-1) \times (m-1)$ 的矩阵,而不是 $m \times m$ 的)
$D_1$ 由于本身就是上三角矩阵,根据行列式性质,$\det D_1=m^n$。
但 $D_2$ 并不是,所以还要转化。
(以下都针对 $D_2$ 矩阵进行转化)
我们首先求出这 $m-1$ 行的和:
$ \begin{bmatrix} n-(m-1) \times \frac{n}{m} & n-(m-1) \times \frac{n}{m} & \cdots & n-(m-1) \times \frac{n}{m} \end{bmatrix} $
其次把上述矩阵直接替换到第一行:
$ \begin{bmatrix} n-(m-1) \times \frac{n}{m} & n-(m-1) \times \frac{n}{m} & \cdots & n-(m-1) \times \frac{n}{m} \\ -\frac{n}{m} & n-\frac{n}{m} & \cdots & -\frac{n}{m} \\ \vdots & \vdots & \ddots & \vdots \\ -\frac{n}{m} & -\frac{n}{m} & \cdots & n-\frac{n}{m} \end{bmatrix} $
发现第一行都是一样的,所以我们就把第一行统一除以 $n-(m-1) \times \frac{n}{m}$,行列式也除以了 $n-(m-1) \times \frac{n}{m}$,所以 $D_2$ 的行列式其实是下述矩阵的行列式乘上 $n-(m-1) \times \frac{n}{m}$:
$ T= \begin{bmatrix} 1 & 1 & \cdots & 1 \\ -\frac{n}{m} & n-\frac{n}{m} & \cdots & -\frac{n}{m} \\ \vdots & \vdots & \ddots & \vdots \\ -\frac{n}{m} & -\frac{n}{m} & \cdots & n-\frac{n}{m} \end{bmatrix} $
(以下暂时换为针对 $T$ 矩阵进行转化)
我们把第一行全部乘上 $\frac{m}{n}$,然后加到下面每一行:(即把下面每一行内的 $-\frac{n}{m}$ 都删掉)
$ \begin{bmatrix} 1 & 1 & \cdots & 1 \ 0 & n & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & n \end{bmatrix} $
此时就是个上三角矩阵了,这个矩阵的行列式 $\det T=n^{m-2}$,显然。
但 $\det D_2=(n-(m-1) \times \frac{n}{m}) \times (\det T)$,所以我们转化一下式子:
(以下省略 $\det D_2=$)
带入 $\det T$:
$(n-(m-1) \times \frac{n}{m}) \times n^{m-2}$
拆括号:
$n \times n^{m-2}-(m-1) \times \frac{n}{m} \times n^{m-2}$
简化式子:
$n^{m-1}-(m-1) \times \frac{n}{m} \times n^{m-2}$
拆开分数:
$n^{m-1}-(m-1) \times \frac{1}{m} \times n \times n^{m-2}$
即:
$n^{m-1}-(m-1) \times \frac{1}{m} \times n^{m-1}$
拆括号:
$n^{m-1}-(m \times \frac{1}{m}-\frac{1}{m}) \times n^{m-1}$
即:
$n^{m-1}-(1-\frac{1}{m}) \times n^{m-1}$
拆括号:
$n^{m-1}-(n^{m-1}-\frac{1}{m} \times n^{m-1})$
拆括号:
$n^{m-1}-n^{m-1}+\frac{1}{m} \times n^{m-1}$
即:
$\frac{1}{m} \times n^{m-1}$
但还没完,答案是 $(\det D_1) \times (\det D_2)$,所以需要推导一下:
带入:
$(m^n) \times (\frac{1}{m} \times n^{m-1})$
拆括号:
$m^n \times \frac{1}{m} \times n^{m-1}$
即:
$m^{n-1} \times n^{m-1}$
所以其实这题的代码很短,只用算 $m^{n-1} \times n^{m-1}$ 的值即可。
*注:这道题原题是M2733,另一种用Prufer序列证明这个答案的方法见本题写的题解,在题解文件夹内。